Why 'Temperature' in AI Isn't Just a Metaphor
- Introduction
- A Quick Detour to Physics Class
- AI Models and Their Secret Physics Habit
- Temperature = How Wild You Want Your AI to Be
- Visualizing the Heat
- The Universe Loves Balance (and So Does AI)
- Closing Thought
- References
Introduction
Ever notice how people say “Let’s increase the temperature” when they want their AI model to sound more creative?
Sounds poetic, right? Like we’re literally “heating up” the model until it starts dreaming.
But it turns out that’s not just a metaphor. It’s actual, hard-core physics sneaking into machine learning.
Let’s unpack why turning up temperature in your AI model feels a lot like shaking up atoms in a hot gas.
A Quick Detour to Physics Class
In the 1800s, Ludwig Boltzmann, a man obsessed with how particles behave, gave us a formula that changed everything:
\[p(\text{system } i) = \frac{\exp(-\beta E_i)}{\sum_j \exp(-\beta E_j)}\]Where:
- $E_i$ = energy of state $i$
- $\beta = 1 / kT$ (the inverse temperature)
- $k$ = Boltzmann constant
- $T$ = absolute temperature
At low temperature, the system prefers the lowest-energy state: stable and predictable. At higher temperatures, it starts exploring other possibilities: a bit more chaotic, a lot more interesting.
Let’s make that concrete.
Example: People and Chairs
Imagine a room with ten people and two chairs.
When it’s cold, the first two people who sit down will stay put. No one wants to move. The system is calm and low-energy.
As the room warms up, people start shifting around. Someone stands, someone else sits. The overall situation looks the same (two people sitting), but who is sitting keeps changing.
When it’s really hot, everyone’s moving constantly. The scene becomes unpredictable; there are many possible “arrangements” happening over time.
That’s what Boltzmann captured: temperature increases randomness by letting the system explore more configurations instead of staying stuck in just one.
AI Models and Their Secret Physics Habit
Here’s the twist: When your model tries to predict the next word, it assigns a score (called a logit) to every possible word.
Then it converts those scores into probabilities using the softmax function:
\[P_i = \frac{e^{\text{logit}_i / T}}{\sum_j e^{\text{logit}_j / T}}\]Look familiar? It’s literally the Boltzmann distribution, just wearing machine learning clothes.
Temperature = How Wild You Want Your AI to Be
Low T (say 0.2): Model gets cautious. It always picks the “safest” word.
“The cat sat on the mat.”
Predictable. Stable. Boring.
Medium T (around 0.8):
“The cat sat on the window ledge, watching the rain.”
Still makes sense, but more expressive.
High T (like 1.5):
“The cat orchestrated a revolution against the vacuum cleaner.”
Chaotic genius energy.
Visualizing the Heat
Let’s see what happens when we crank the temperature up or down. Imagine we have these initial logit scores for possible next words: cat (2.8), dog (2.0), bird (1.5), fish (1.0), mouse (0.5), and other (0.0).
Now watch how different temperatures reshape the probability distribution:
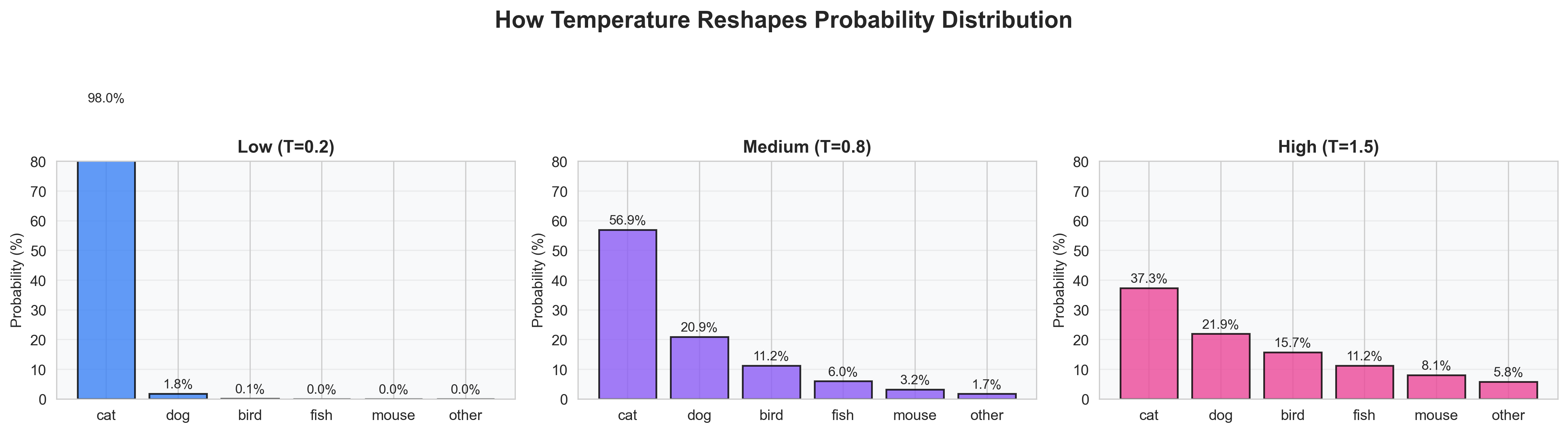
At low temperature (0.2), the model is highly confident. “Cat” dominates with 73.1%. The distribution is sharp and spiky, like a frozen crystal where particles barely move.
At medium temperature (0.8), things get more balanced. “Cat” drops to 37.8%, “dog” rises to 27.8%, and multiple options get reasonable consideration. It’s like a warm cup of tea: gentle movement, but still structured.
At high temperature (1.5), the distribution becomes nearly flat. “Cat” is only 24.5%, barely ahead of “dog” at 20.2%. The model is willing to take creative risks: pure boiling chaos.
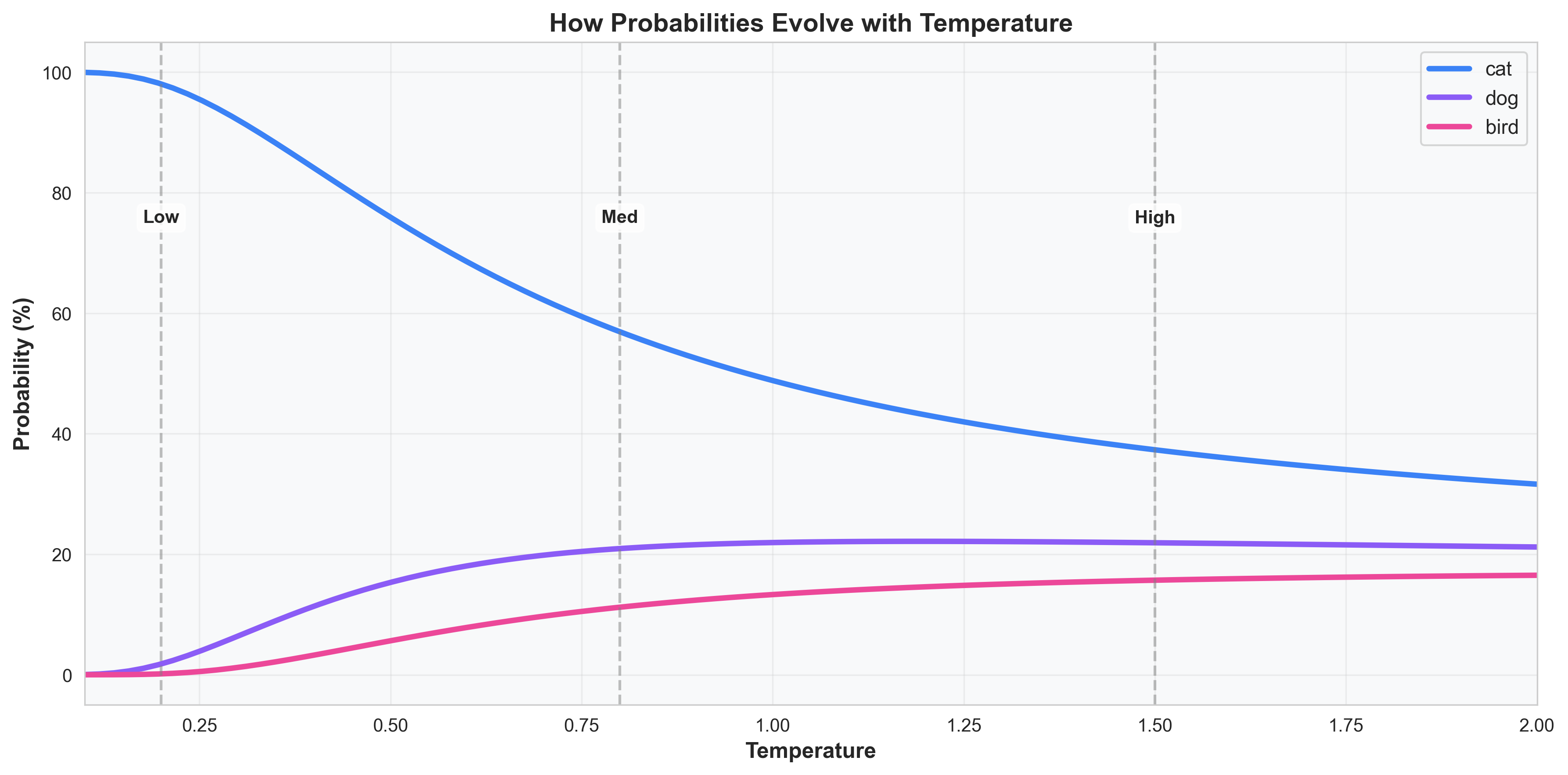
This curve shows the beautiful continuous transition. As temperature rises from 0.1 to 2.0, the top choice gradually loses its dominance while the underdogs gain ground. It’s a perfect visual representation of how thermal energy democratizes possibilities.
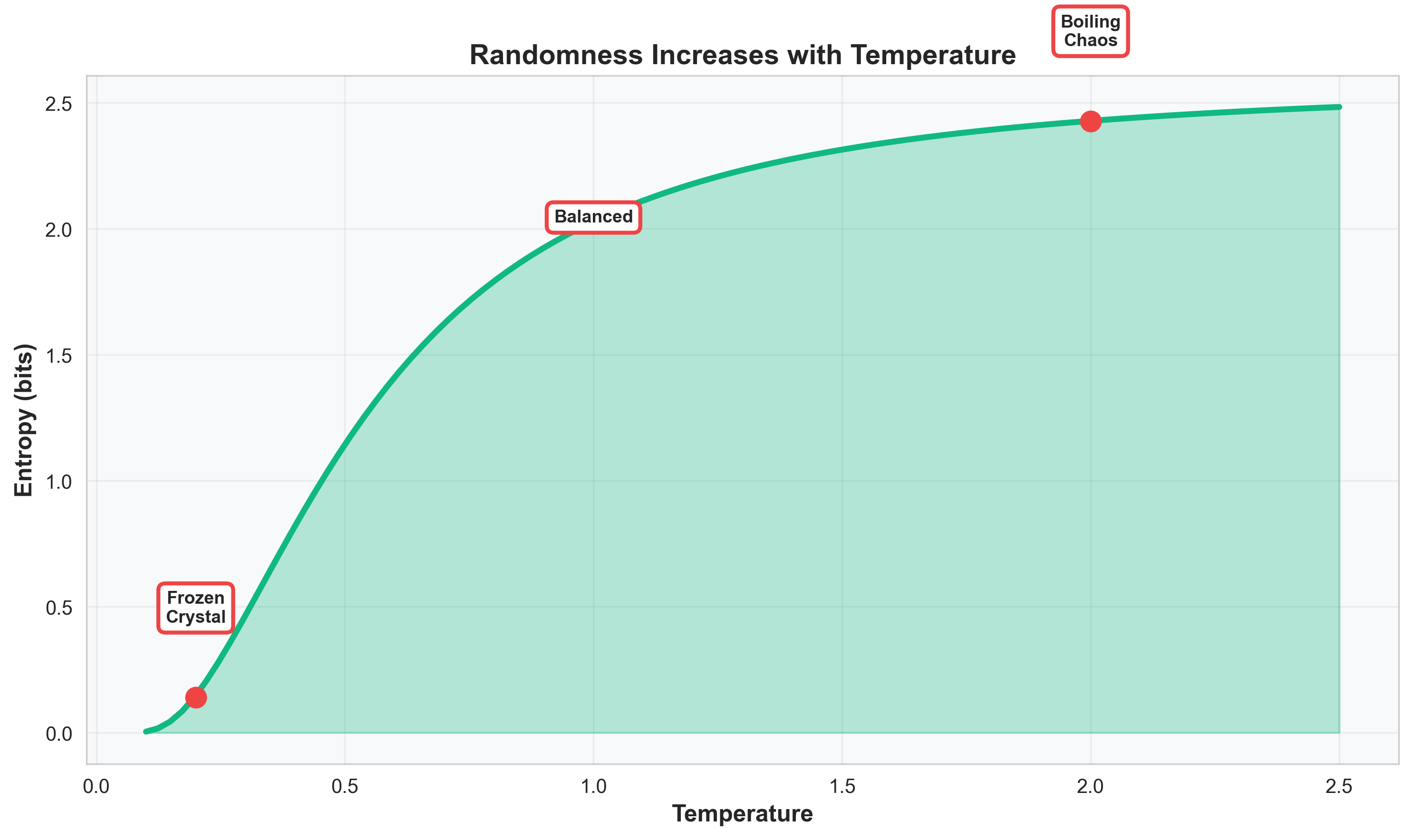
The entropy curve quantifies what we’ve been seeing: randomness literally increases with temperature. Low temperature means low entropy (the system is predictable). High temperature means high entropy (anything can happen).
It’s just like atoms at different temperatures: cold means neatly aligned with minimal movement; hot means dancing everywhere with high energy.
| Temperature | Behavior | Analogy |
|---|---|---|
| 0.2 | Deterministic | A frozen crystal |
| 1.0 | Balanced | Warm cup of tea |
| 2.0 | Random | Boiling chaos |
The Universe Loves Balance (and So Does AI)
There’s something poetic about this. At low temperature, the system (or model) seeks equilibrium: it picks what’s most likely, just like atoms resting in their lowest-energy state.
Every time you tweak the temperature knob, you’re not just adjusting a model setting. You’re echoing Boltzmann’s law of nature.
The same law that explains:
- Why stars burn
- Why ice melts
- And now… why your model sometimes says “quantum kittens are revolutionizing linguistics” 🐱⚛️
Closing Thought
So next time you see “temperature = 0.7” in a prompt or config file, remember: that’s not just code. That’s the physics of imagination.
We’ve been using the math of molecules to make machines dream. And that’s… kind of beautiful, isn’t it?
References
- Boltzmann, L. (1872). Further Studies on the Thermal Equilibrium of Gas Molecules
- Goodfellow, I., Bengio, Y., & Courville, A. (2016). Deep Learning. MIT Press
- Alammar, J. The Illustrated Softmax
- Olah, C. Neural Networks, Softmax, and Temperature
Enjoy Reading This Article?
Here are some more articles you might like to read next: